
Оберт а тельное рух е ня твердого тіла, 1) обертальний рух навколо осі - рух твердого тіла, при якому будь-які дві його точки А. і В залишаються весь час нерухомими (див. Рис.). Пряма AB, що проходить через ці точки, називається віссю обертання; всі точки тіла при Ст д. описують кола в площинах, перпендикулярних до осі обертання, і з центрами, що лежать на цій осі. Тіло, яка вчиняє В. д., Має одну ступінь свободи і його положення визначається кутом φ між проведеними через вісь обертання нерухомою напівплощиною і напівплощиною, жорстко пов'язаної з тілом і обертається разом з ним. Основні кінематичні характеристики В. д. Тіла - його кутова швидкість ω і кутове прискорення ε. Для будь-якої точки тіла, віддаленої від осі на відстані h, лінійна швидкість v = h ω, дотичне прискорення w τ = h ω, нормальне прискорення wn = h ω2 і повне прискорення

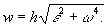
Основними динамічними характеристиками В. д. Тіла є його кінетичний момент щодо осі обертання Kz = Iz ω (див. Момент кількості руху ) І кінетична енергія Т = 1/2 Iz ω2, де Iz - момент інерції тіла щодо осі обертання. Закон обертання визначається з основного рівняння Iz ε = Mz, де Mz - момент, що обертає (див. момент сили ).
2) Обертальний рух навколо точки (або сферичне рух) - рух твердого тіла, при якому якась одна його точка Про залишається нерухомою, а всі інші точки рухаються по поверхні сфер, що мають центр в точці О. При такому В. д. Тіла будь-яке його елементарне переміщення являє собою елементарний поворот навколо деякої осі, що проходить через точку О і називається миттєвою віссю обертання. Згодом ця вісь, на відміну від нерухомої, безперервно змінює свій напрямок. В результаті В. д. Тіла складається з серії елементарних поворотів що довкола безперервно міняють свій напрям миттєвих осей. Приклад такого Ст д. Тіла дає рух гіроскопа .
С. М. Тарг.
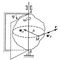
Малюнок до ст. Обертальний рух.

