- 1.4.1. інтенсивність поля Амплітуда поля не може безпосередньо спостерігатися або вимірюватися,...
- Додавання когерентних полів
- Додавання некогерентних полів
- 1.4.3. Квазімонохроматіческое і поліхроматичне поле
- 1.4.4. Найпростіші монохроматические хвилі
- плоскі хвилі
- сферичні хвилі
1.4.1. інтенсивність поля
Амплітуда поля не може безпосередньо спостерігатися або вимірюватися, так як поле дуже швидко змінюється в часі з частотою 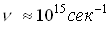 і
і  , А будь-які приймачі випромінювання мають значно більшу, ніж період коливань, час інерції
, А будь-які приймачі випромінювання мають значно більшу, ніж період коливань, час інерції  . Тому реєструється лише усереднена в часі величина - інтенсивність поля
. Тому реєструється лише усереднена в часі величина - інтенсивність поля  .
.
з рівнянь Максвелла випливає, що інтенсивність пропорційна квадрату амплітуди поля, тобто дорівнює квадрату модуля комплексної амплітуди (твору комплексної амплітуди на величину, комплексно сполучену їй):
Можна виміряти квадрат модуля комплексної амплітуди, але неможливо виміряти фазу і ейконал поля - при реєстрації поля вони губляться. Для збереження інформації про фазу (ейконале) вимагається вимірювання інтенсивності поля, складаються з декількох полів.
1.4.2. Спостережувані величини при додаванні полів
При складанні двох полів 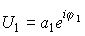 (з фазою
(з фазою 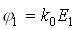 ) і
) і  (з фазою
(з фазою  ), Сумарну інтенсивність можна представити у вигляді:
), Сумарну інтенсивність можна представити у вигляді: 
Таким чином, сумарна інтенсивність записується у вигляді рівняння інтерферограмми:
де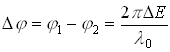 - різниця фаз поля.
- різниця фаз поля.Явище, що виникає при складанні двох полів, називається інтерференцією, а інтерферограмма - це картина, яка спостерігається при інтерференції.
Додавання когерентних полів
Когерентні поля характеризуються тим, що різниця фаз (ейконалов) двох полів залишається постійною за час інерції приймача.
В цьому випадку сумарна інтенсивність визначається виразом (1.4.2), а картина розподілу інтенсивності являє собою чергування темних і світлих смуг, конфігурація яких залежить від зміни різниці фаз 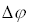 .
.
Введемо поняття референтного (еталонного) поля, яке має відому картину фаз. При порівнянні з ним виявляються параметри іншого поля (інтенсивність і фаза). Реєстрована картина взаємодії двох полів, одне з яких референтное, називається голограмою. Голограма - це запис повної інформації про поле, тобто його комплексної амплітуди. Інтерферограмма і голограма - способи запису комплексної амплітуди поля шляхом порівняння його з еталонним полем.
Додавання некогерентних полів
Якщо різниця фаз полів змінюється випадковим чином багато разів за час реєстрації, то поля є некогерентного. При реєстрації сумарної інтенсивності її значення за часом усереднюються: 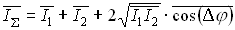 (1.4.4)
(1.4.4)
У вираженні (1.4.4) 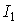 і
і 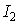 - постійні, їх можна не усереднювати, а
- постійні, їх можна не усереднювати, а  , Тоді, отримаємо вираз для складання двох некогерентних полів:
, Тоді, отримаємо вираз для складання двох некогерентних полів:
1.4.3. Квазімонохроматіческое і поліхроматичне поле
Поле, що випромінюється реальними джерелами світла, не буває строго монохроматическим . Воно буває лише дуже близьким до повної монохроматичности, тобто квазімонохроматіческім. поліхроматичне поле 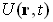 можна вважати сумою (суперпозицією) монохроматичних складових, а інтенсивність такого сумарного поля обчислювати таким чином:
можна вважати сумою (суперпозицією) монохроматичних складових, а інтенсивність такого сумарного поля обчислювати таким чином:  (1.4.6)
(1.4.6)
де  - розподіл інтенсивності монохроматичної складової по довжинах хвиль,
- розподіл інтенсивності монохроматичної складової по довжинах хвиль,  - вагова спектральна функція (наприклад спектральна чутливість приймача),
- вагова спектральна функція (наприклад спектральна чутливість приймача), 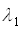 і
і 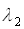 - реальні межі діапазону випромінювання.
- реальні межі діапазону випромінювання.
На Рис.1.4.1 показаний приклад графіка розподілу інтенсивності і ваговій спектральної функції.
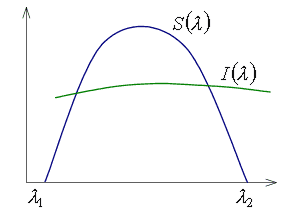
Рис.1.4.1. Інтенсивність і вагова спектральна функція.
1.4.4. Найпростіші монохроматические хвилі
Розглянемо два типи хвиль: плоскі хвилі і сферичні хвилі.
плоскі хвилі
Плоскі хвилі (plane waves) називаються так тому, що вони мають плоскі хвильові фронти (ріс.1.4.2).
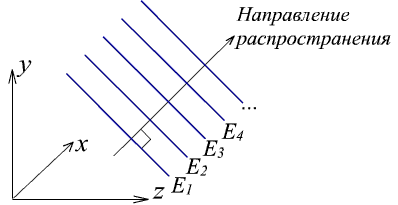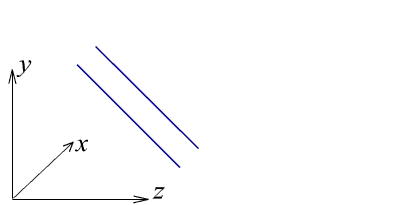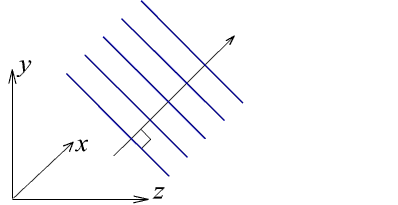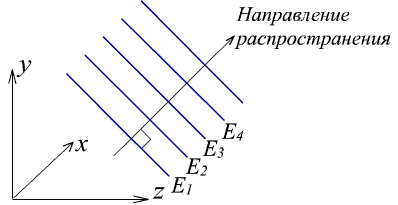
Ріс.1.4.2. Плоскі хвилі.
Хвильовий фронт - це поверхня в просторі, на якій ейконал поля (або фаза) має однакові значення:
Різним значенням постійної 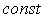 відповідають різні хвильові фронти. якщо міняти
відповідають різні хвильові фронти. якщо міняти  , То хвильовий фронт буде переміщатися в просторі, переходячи з одного стану в інший. Поле поширюється в бік збільшення
, То хвильовий фронт буде переміщатися в просторі, переходячи з одного стану в інший. Поле поширюється в бік збільшення  .
.
Напрямок поширення світла перпендикулярно хвильовим фронтах, як показано на ріс.1.4.2.
Довжина вектора, що показує напрямок, може бути обрана по-різному:
де 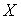 ,
,  ,
,  - напрямні косинуси (помножені на показник заломлення середовища косинуси кутів між осями координат і напрямком поширення). Складові променевого вектора
- напрямні косинуси (помножені на показник заломлення середовища косинуси кутів між осями координат і напрямком поширення). Складові променевого вектора  і
і 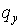 називають також просторовими частотами плоскої хвилі.
називають також просторовими частотами плоскої хвилі.
Всі ці вектори ( 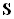 ,
, 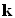 ,
,  ) Мають однаковий напрямок (в сторону поширення поля), але різну довжину.
) Мають однаковий напрямок (в сторону поширення поля), але різну довжину.
Рівняння плоскої хвилі має такий вигляд:
Для плоскої хвилі амплітуда постійна, змінюється тільки ейконал , Який можна записати як рівняння площині:
З аналітичної геометрії слід, що при такому описі ейконалу хвильовий фронт плоский і перпендикулярний вектору поширення, тобто оптичному променевому вектору  . Плоскі хвилі чудові тим, що будь-яке складне поле можна представити у вигляді сукупності плоских хвиль. Тому ці хвилі є універсальним базисом для опису світлових полів.
. Плоскі хвилі чудові тим, що будь-яке складне поле можна представити у вигляді сукупності плоских хвиль. Тому ці хвилі є універсальним базисом для опису світлових полів.
сферичні хвилі
Сферичні хвилі (spherical waves) мають хвильовий фронт у вигляді концентричних сфер (ріс.1.4.3).
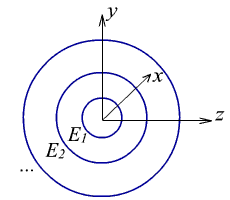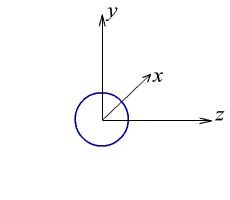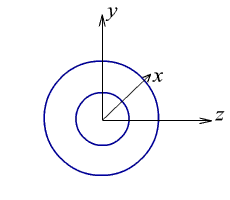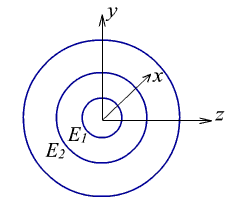
Ріс.1.4.3. Сферичні хвилі.
Помістимо систему координат в центр, тоді отримаємо такі вирази для комплексної амплітуди і ейконалу сферичної хвилі.
Рівняння сферичної хвилі:
Рівняння ейконалу сферичної хвилі:
де 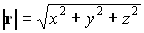 - це довжина радіус-вектора точки в просторі.
- це довжина радіус-вектора точки в просторі.
Сферичні хвилі так само, як і плоскі, можуть бути використані для представлення складних полів, крім того, плоскі хвилі можна вважати окремим випадком сферичної хвилі з нескінченно малою кривизною хвильового фронту.

